Menu

Learning Java

Articles
Author Profiles
Lessons
FAQ's
Books
Newsletter
Tutorials
Talk Java!

Using Java

Applets
JavaBeans
Servlets
Resources
Discuss Java

Looking for Java resources? Check out the Java Coffee Break directory!

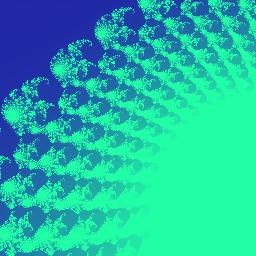
"The Mandelbrot set? I know. They are on bookshelves in the libraries."

"Glamorous pictures! But I don't know how to draw them."

"How long does it take you to become a virtual artist, Bill?"

These are the typical questions people would probably ask about when they first glance the fractal images below or even better ones like those that can be found elsewhere. The first time when I myself read a book on fractals, I had thought that heavy efforts must have been spent on drawing those pictures, which had effectively made me timid until recently.

How easy it is to become a virtual artist!

Because of my current job (computer simulation for biomolecules), I am always concerned with computer graphics. I realized that if I were to write a graphics library, which is to be used to assemble biochemical systems on screen in my own style, I must know more about Java 2D and 3D APIs. So I looked up the Java documentation for the details about how graphics is rendered in Java. A week later I ended up with the AWT applet and Swing app both of which you can find on this page.

I am not going to present here all aspects of Java graphics. In what follows I will talk about only the classes necessary to display a fractal image. So let's get started.

Graphics Format

One of the ways in which an image is described is assigning to the pixels values that represents the graphical properties such as RGB colors and transparency (alpha value). These properties can be stored in an int array pixels[width*height] (note that it is NOT a two dimensional array pixels[width,height]), where width and height are the width and height (in pixels) of the rectangular area in a browser or application window where the image is to be displayed. An element of the array pixels[] is a 32 bit integer which is bitwisely stored the RGB colors and alpha value in the following way

	alpha	red	green	blue
pixels[i,j]=	xxxxxxxx	xxxxxxxx	xxxxxxxx	xxxxxxxx

where x is binary 0 or 1. The maximum alpha value 0xff corresponds to completely transparent, and the minimum 0x00 corresponds to completely opaque. The color compositions are like 256 RGB for HTML, for example, 0xffffff is white, 0x000000 is black, 0xff0000 is red, 0x00ff00 is green, 0x0000ff is blue, etc. In terms of data format, an image is just an array like this. But you may have heard different types of graphics formats such as JPEG and GIF. These more popular formats are actually the results of encoding the raw RGB format in different ways. One of the major reasons for the existence of these encoders is that they are efficient ways of compressing data of images without lowering down the quality of images to an extent sensible to human eyes.

So how to assign color to a pixel? Easy. Suppose you would like the (i,j) pixel of your image to be as colorful as "#78c5a1" (I assume that you know how to define a 256 RGB color in HTML, so I follow the convention), do like this

  int alpha=0xff; 
  int red=0x78; 
  int green=0xc5; 
  int blue=0xa1; 
  pixels[j*width+i]=alpha<<24 | red<<16 | green<<8 | blue; 

The bitwise left shifts send the color numbers and alpha value to the corresponding bit positions, and the bitwise or operator forms the 32 bit integer. If you mistakenly define an int greater than 255, you will still get a color but that's probably something you can't fit into the ordinary RGB mode.

Render an Image

  MemoryImageSource source =  
    new MemoryImageSource(width,height,pixels,0,width); 

This line of code constructs an ImageProducer object which uses an array of integers in the default RGB ColorModel to produce data for an Image object to be created. When you need to update the pixels[] array in an already initialized object source, call the newPixels method

  source.newPixels(0,0,width,height); 

Many AWT components inherit the method createImage which converts a MemoryImageSource object into an Image object

  Image image = createImage(source); 

If you have been a Java programmer for a while and you know a little bit about fractals, to this point, you won't need to read the rest of my article. You know how to render an Image object to an applet with the double-buffered method(if you are still programming with JDK1.0) and design your own widgets to control the image generation. In the following I would just talk about what I have done to explore the Mandelbrot set in line with my private aestheticism.

Explore the Mandelbrot Set

The Mandelbrot set is the domain of convergence of the series built up by a recursion formula of complex number: Z(n)=Z(n-1)*Z(n-1)+C. The points of the complex plane can be classified into two categories: inside the Mandelbrot set or outside. The trick to draw an artistic Mandelbrot set is to assign the color of an outside point according to its "distance" to the Mandelbrot set, which is the number of iterations required to determine if or not it is outside the Mandelbrot set.

At this point we have to define two coordinate systems. One is the one on the screen whose origin is at the upper left corner of the window, the other is the complex plane relative to the Mandelbrot set. I wrote two methods scaleX and scaleY to convert them. A rectangle [-2.0, 1.0, -1.5, 1.5] in the latter well confines the whole Mandelbrot set.

I decided to allow the applet to be able to magnify the Mandelbrot set up to a scale of 10000000X. Due to self similarity, the pattern will likely be alike. If one doesn't set a limit to the magnification ratio the applet might crash when the size of the window on the Mandelbrot set becomes numerically too small.

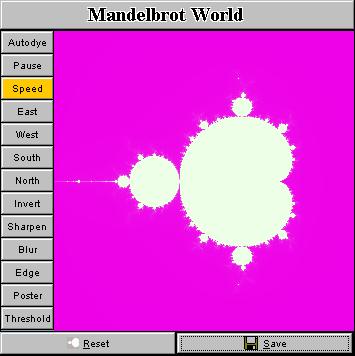
After the applet is invoked, it will display the full Mandelbrot set (the Mandelbrot Dinosaur), namely, the window [-2.0, 1.0, -1.5, 1.5]. When the user clicks somewhere the applet, it will capture the coordinates of the mouse click event (x,y) and set it the center of the new window [x-length/zoomin, x+length/zoomin, y-length/zoomin, y+length/zoomin], where length is the length of the previous window in the Mandelbrot coordinate system, zoomin is the magnification after a click. Then this part of the Mandelbrot set is drawn on the window. After about ten clicks, the bounds are reset to [-2.0,1.0,-1.5,1.5] so that the user can start a fresh round of exploration into the Mandelbrot set. All these events are controlled by a single thread implemented by the applet. (Although in the following code the thread looks redundant, it was left there for you to add your own methods to create spontaneously evolving images.)

Clicks into the depth of the Mandelbrot world. Red and white are my favorite colors.

Click here to view the source code for the Mandelbrot fractal applet

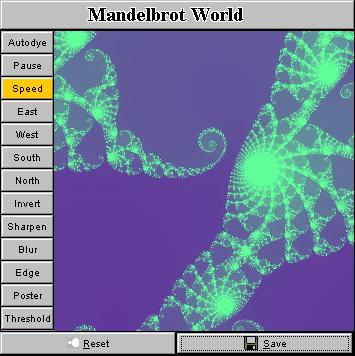
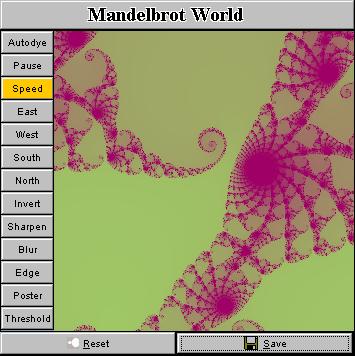
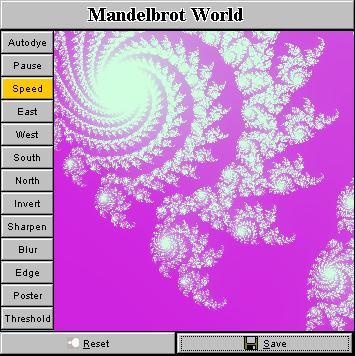
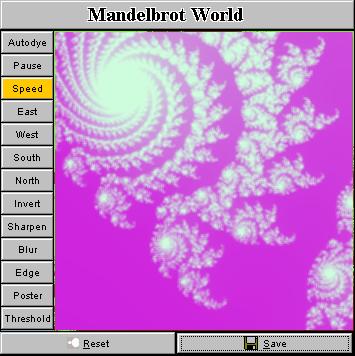
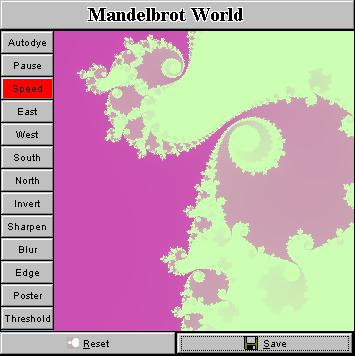
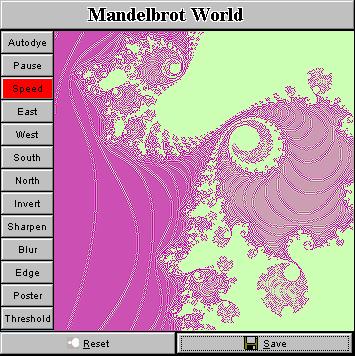
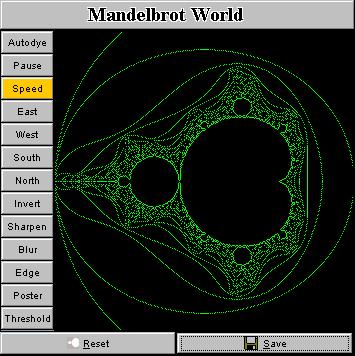
That's it. Isn't it easy?

I exhibit in the above mosaic a number of snapshots taken from this tiny applet. In principle, you can obtain as many fractal pictures as you want, every pattern you will get is likely different from the ones that have already been in existence (though they could look similar), and the price is only a few mouse clicks!

Conclusion

With such a handy applet, you don't need to navigate around the Internet to those fractal galleries which have tons of high-resolution pictures to jam your bandwidth. Just load and click the applet, it will guide you into the beautiful world of fractal. Digest Java also have generously published the code here (other Java applets running on the Internet don't provide this courtesy).

So you have seen how easy it is to draw fractals in your fascinating way. This is really nothing difficult. The charm and beauty don't come from the fractal pictures but the Java language which makes the deployment of a fractal generator on the Internet such a painless job.

A question that is puzzling me now is that: Is it possible to do this with JavaScript? Bruce Eckel claims in his book "Thinking in Java" that 80% of web programming can be done with script languages like JavaScript or VBscript. But can fractals be played with JavaScript in such an elegant way?

Supplement

A standalone app written in Java 2, which has a simple user interface as shown below, has been released (You can download it below. Currently you can only run it on a DOS console, or you can run it as an applet in browser. Sorry I haven't built a Java-Win32 hybrid program). The basic idea is to build a random fractal image generator which produces a background image to be adopted as an input to more sophisticated and professional graphics tools like Photoshop and Corel Photo Paint. Internet artists can then post-process a fractal image and add whatever they need to put on top of such a fractal background to create a desired effect.

Here are some screenshots of the app. I also install some useful image processing functionalities, so that you don't need to rely on a postprocessor like Photoshop for simple image manipulations. For example, you can invert the image on screen

Two images negative to each other.

Blur it.

Sharpen sharpen sharpen, the fourth time you get this impressionistic effect.

Edge-detect the Mandelbrot set.

And, of course, you are able to shift the Mandelbrot window in four different directions: east, west, north and south. There is also a two-speed gear in control of the drift speed. The program can therefore be used as a screensaver if the size is enlarged to cover the whole screen.

Downloads

About the author

Qian Xie is a physicist at the National Laboratory of Materials Simulation and Design, Tsinghua University, China. His research interests includes computer simulation technologies and computer-aided design in physics, chemistry, and molecular biology. In his spare time, he is learning the Java programming language and using it to write educational software. He can be reached via email at qianxie@hotmail.com, or his personal website. 

You can also visit Digest Java's Java Molecular Dynamics, which is an educational tool for studying how a system of particles with soft-core interactions evolves. If you have no interest in physics, I will show you how collective motion of particles resembles the dynamics of a stock market.

Back to main